The cubic function is a function that is given by a polynomial of the third degree, and has the form of y=ax^3+bx^2+cx+d, where a, b, c, d are some numbers, (a≠0).
The graph of a cubic function is a cubic parabola whose vertex is at (0;0).
The scope and scope of a function are a set of real numbers. The function is incremental.
Special case: y=ax^3, (а≠0). Located in I and III quarters at a>0, in II and IV quarters at a<0.
The cubic function of the form y=a(x-m)^3 shifts along the x-axis when the m coefficient changes. The cubic function of the form y=ax^3+n shifts along the Y axis when the coefficient of n changes.
Plot a graph of the cubic function online
Example cubic function graph:
у=x^3
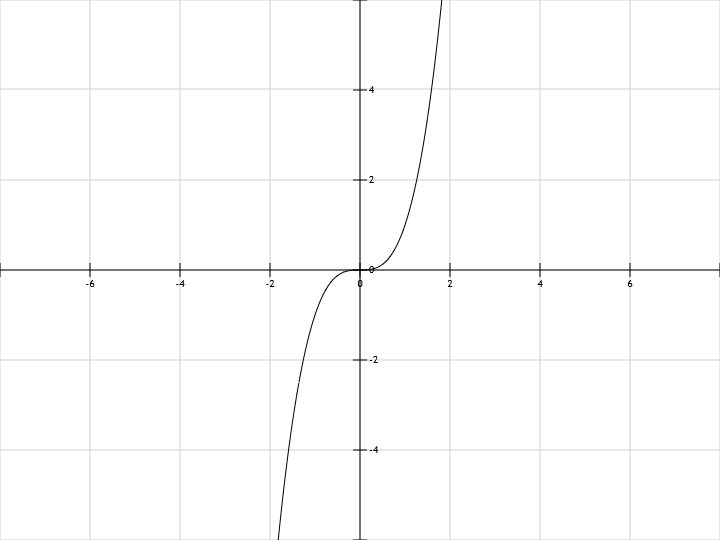
у=-x^3
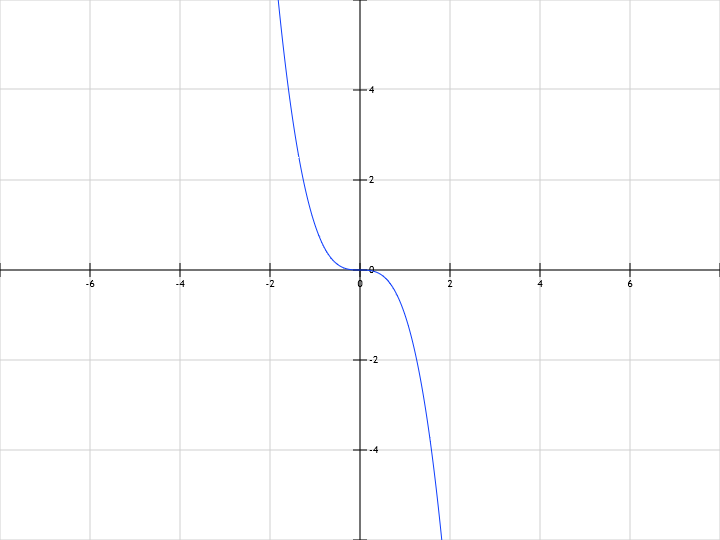
у=1/2x^3
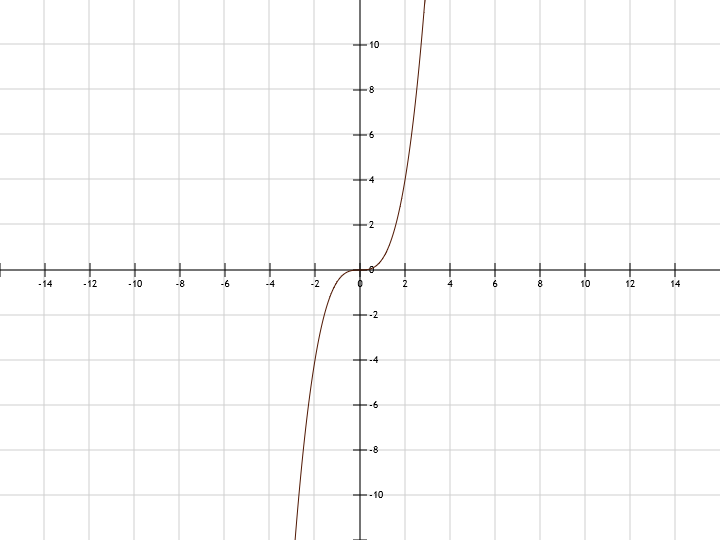
у=x^3+2
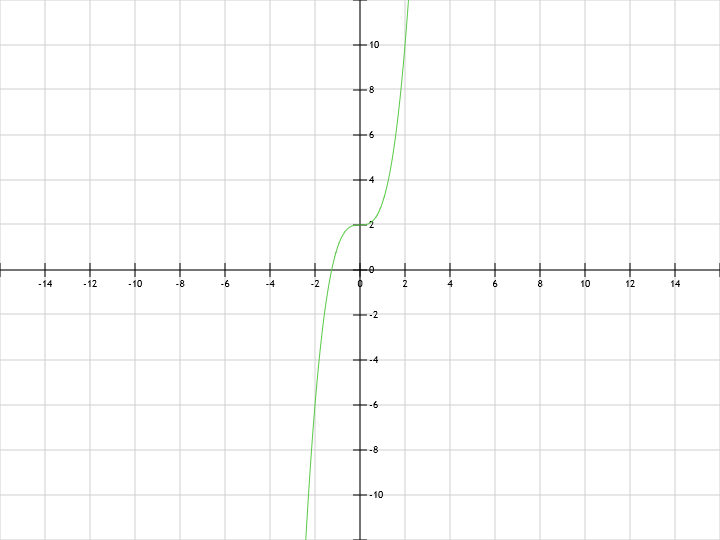
у=2x^3+x^2+6x+7

All graphics are built with our graphical calculator