Modal functions have a module that reverses any value of a function to positive.
For example, y = |x|, y = |x^2 – 8x + 12| etc.
The variable module is defined as follows:
|x| = x, if х ≥ 0,
|-x| = x, if x < 0.
When constructing a graph, all values are obtained positive, which means that the graph is on the top of the axis X. The part that should be on the negative section X is reflected and continues with positive values.
If the action is not part of the module sign (for example, y=|x|-3), then the center of the graph on the Y axis is offset by 3 units in this case.
Plot a graph of the modulo function online
Example modal function graph:
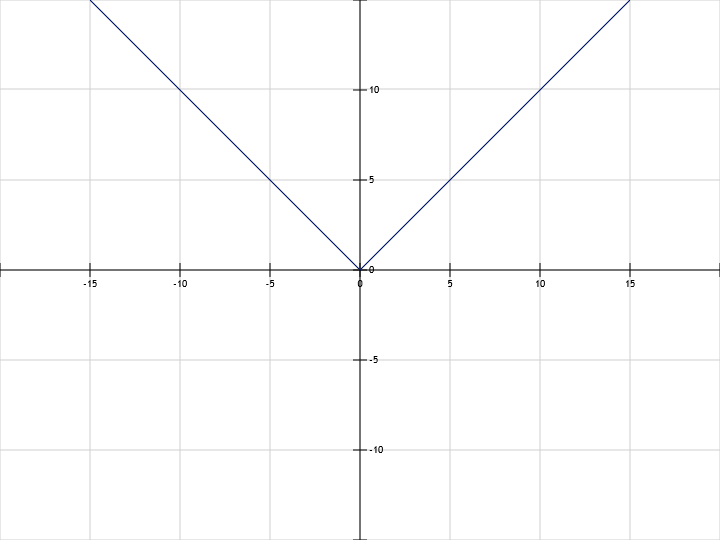
y=|x| abs(x)
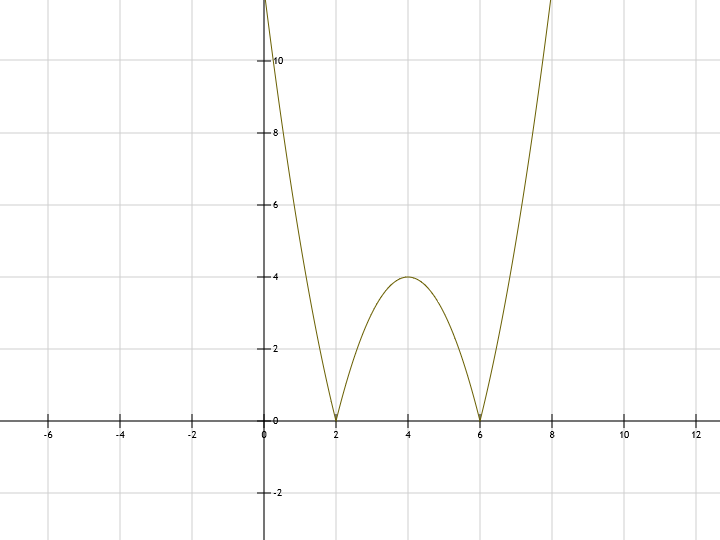
y = |x^2 – 8x + 12| abs(x^2-8x+12)
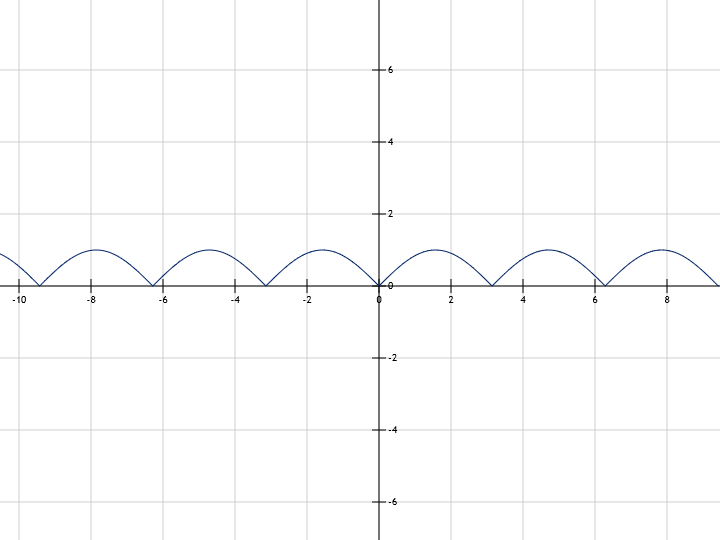
y=|sin(x)| abs(sin(x))
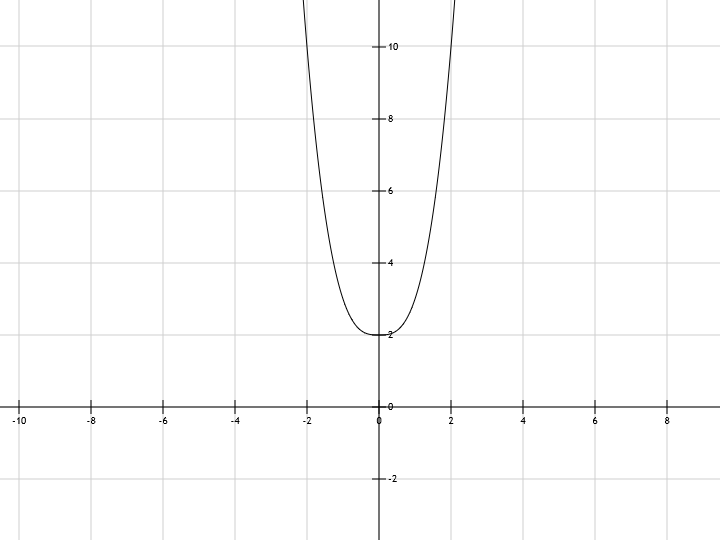
y=|x^3|+2 abs(x^3)+2
y=|tan(x)| abs(tan(x))
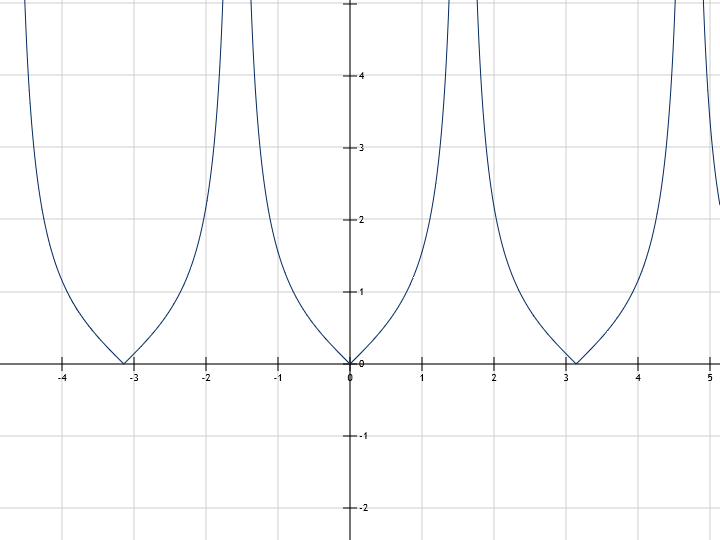
All module graphs are built with our graphical calculator