The cotangent function is y = ctg(x).
The graph of the function is called the cotangensoid. The function is periodic, that is, repeated. The cotangensoid period is defined as T= π.
The function is descending. The branches of the graph are at the same distance from each other (π), being “parallel” with respect to the Y axis.
The scope and scope of the function are all valid numbers.
Example cotangent function graph:
y = ctg(x) cot(x)
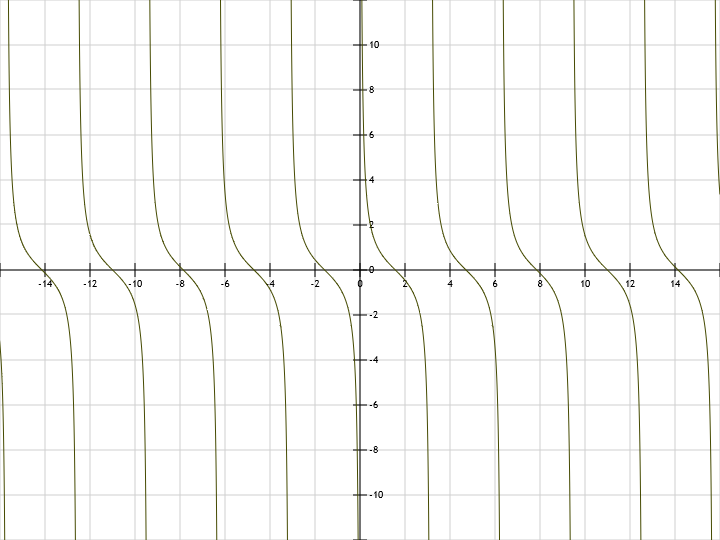
- y = – ctg(x) -cot(x) the graph is shown horizontally
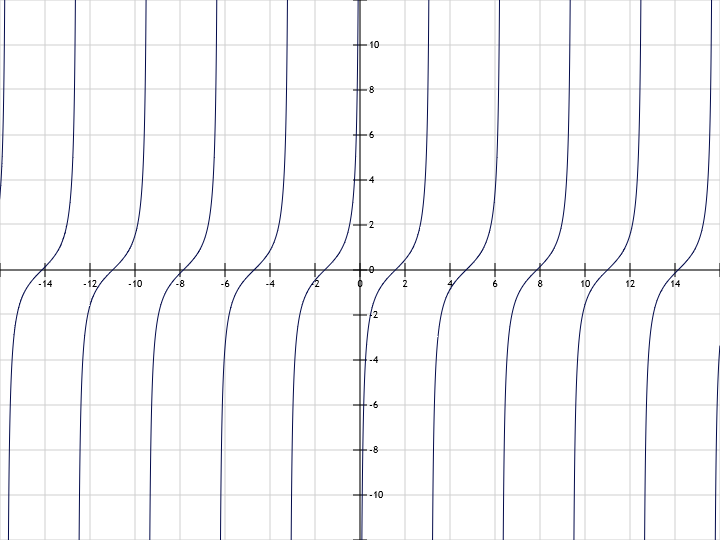
- y = ctg(2x) cot(2x) the graph is “compressed”, the period is defined as T=1/2π
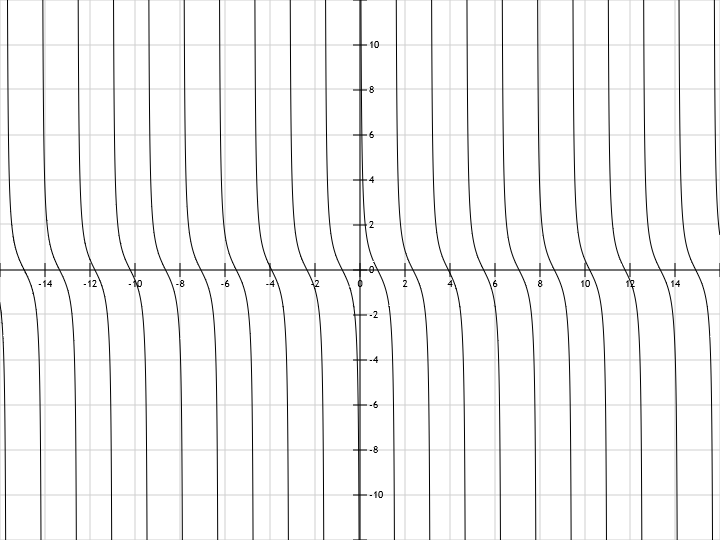
- y = ctg(1/2x) cot(1/2x) – graph “expands” and period – T=2π
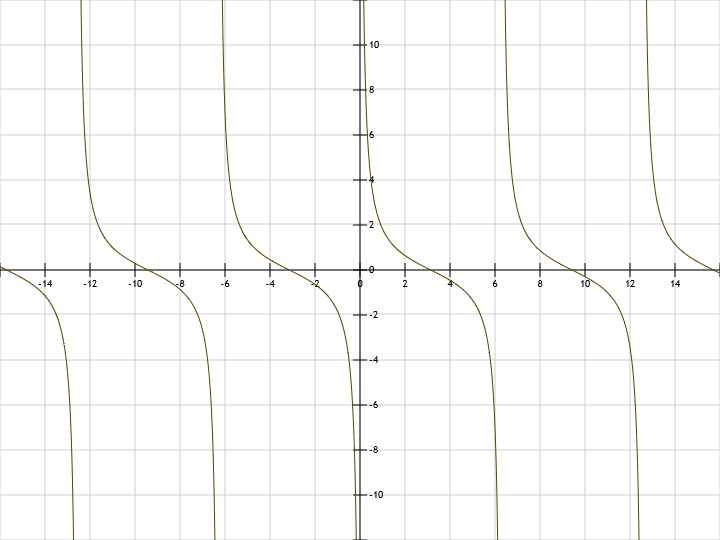
- y = ctg(x)+2 cot(x)+2 the graph is shifted along the axis Y by n steps
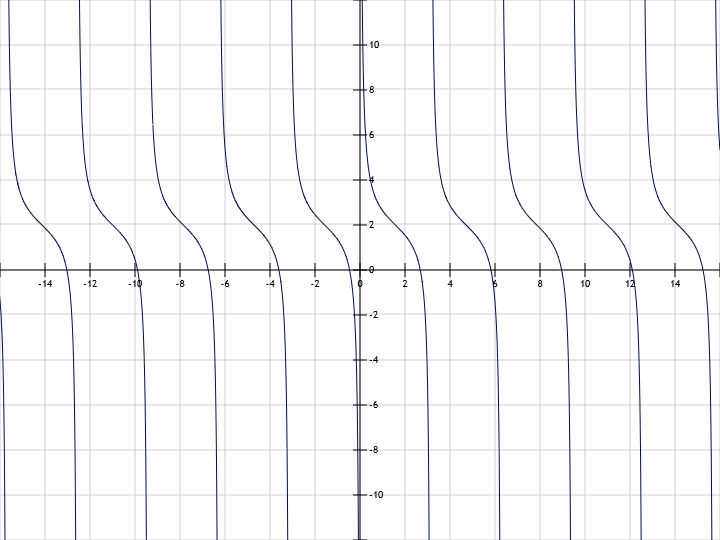
- y = ctg(x+2) cot(x+2) the graph is shifted along the x-axis by 2 steps
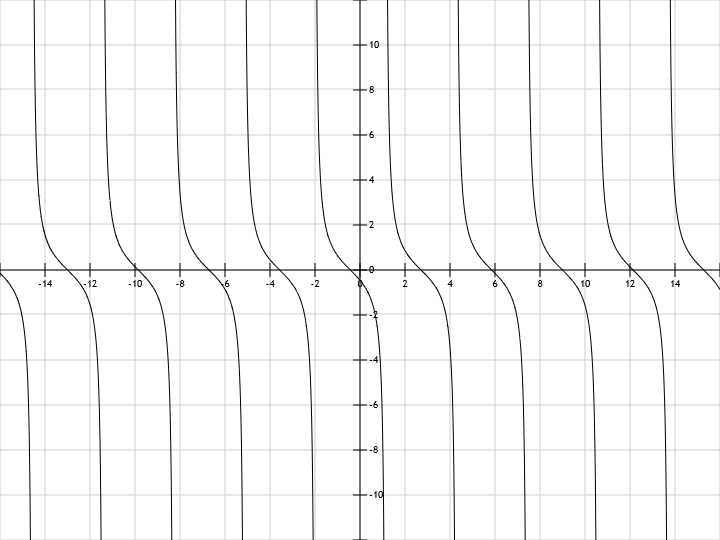
All cotan graphs are built with our graphical calculator
Plot a graph of the cotangent function online